Free-riding, the passing of a course without contributing sufficiently to the end-result of a project, is a common occurrence amongst student groups. To prevent free-riding, some teachers incorporate a peer-to-peer grading system at the end of the course.
However, simply grading fellow students often leads to ambiguous practices, such as students grading all their peers equally (when this does not reflect the actual students’ contribution), everyone giving everyone a high grade, or strong divergence between the grades provided by the free-rider and the rest of the student group.
Below, I present a simple model for an (anonymous) peer-to-peer grading system. The crux of the model is that it is in the best interest of all the students to answer honestly, even when they know they have made an insufficient contribution to the project.

So, here’s how it works!
Each student indicates their peer’s perceived contribution on a 5-point scale, starting from [–] to [++]. On the background, this is converted into numbers, -2 to +2.
The number of plusses and minuses needs to equal zero. So just giving everyone the maximum number of points is not allowed.
If the student thinks everyone contributed equally, then he or she should indicate this with an empty rating. I included a schematic of what such a grading scheme looks like below.
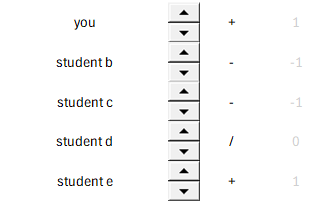
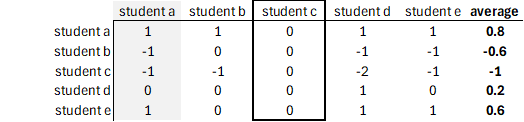
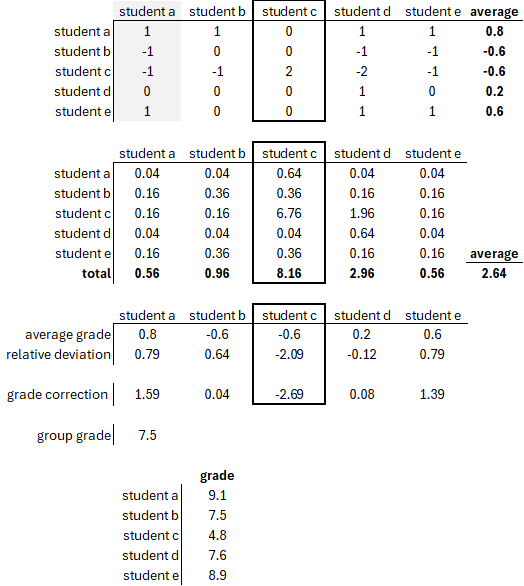
Now, let’s take an example where we have a free-rider student: student c. All other students from the group rate this student as having contributed less to the team, but the student in question has rated everyone equally (0).
Based on this input alone, we can compute an average which could be used (in the appropriate proportion) to correct the total grade of the group. However, this does nothing to prevent the unfair grading of others.
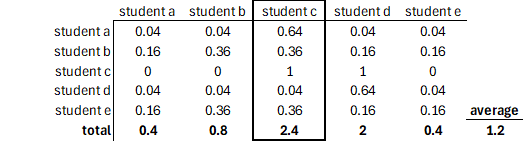
To correct for this, we can calculate the difference (squared) between the grade assigned and the average per student. From that, we can calculate the total deviation per student which indicates how ‘untrue’ the corresponding student’s grading has been.
When we now subtract the average deviation from the total deviation per student, and divide the result by the average deviation, we have a scaled correction factor for the ‘truthfulness’ of the assessment. Students that are below the average standard deviation get a bonus, whereas students that are above it get a penalty.
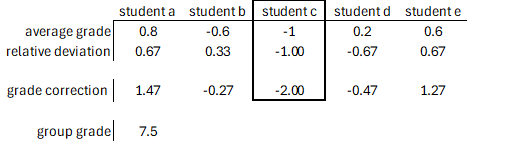
If we incorporate both in a 1:1 fashion, and assume an overall grade of 7.5 for the free-riding student, the latter would be penalized by two points, just barely passing the project (in the Netherlands, that is).
If student a really pulled the cart for this project (and that is how it seems from the initial assessment table), basically compensating for student c, it—to me—does not seem unfair that the student be awarded a 9 instead of a 7.5.
To illustrate the power of the deviation component added to the peer-to-peer assessment model, we can run the whole simulation again, but now the free-riding student gave himself a score of 2 instead of 0. Were this to happen, the student would penalize himself with .7 points, a rather significant penalty for trying to cheat the system!
Would a model like this solve the issue of free-riders? And should you be transparent about the model, or simply say that they should fill in the peer-to-peer assessment truthfully? What issues do you foresee?