Today, I want to share a simple simulation model of a financial market. A financial market is a place where investors can buy and sell financial products. A good example of this is a stock market, where investors can buy and sell company shares (stocks).
To simulate such a market, I will be using agent-based simulation software: AnyLogic. Agent-based models only define the behaviour of agents (in our case, investors) and the environment in which they operate. Agent-based models can show how complex system behaviour emerges from simple agent rules.
You can download and use AnyLogic for free! If you want to follow along and tinker with the model as we go, you can download the software here.
Basic model structure
At the most basic level, the model needs to contain the following elements:
An investment or asset to trade (e.g. a stock).
A market where the asset is traded (e.g. the London Stock Exchange).
Investors that will do the trading.
These agents interact as follows: first, the value of the underlying investment changes. Investors then determine a price for which they are willing to buy or sell the asset. If they own the asset, they put out an ask-order. When they do not own the asset, they will put out bid-order instead.
After all investors have placed their bids and asks, the market will solve the order books. This entails transferring the assets between investors when they agree on the price. Price agreement emerges when the bid price of one agent is equal to, or higher than, the ask price of another.
Let’s take a look at what this would look like in the different model agents.
The investment-agent
Below you can see the core structure of the investment agent. It has three basic variables
Fundamental value: what the investment is actually worth.
Price: the lowest price at which the investment is sold.
Volatility: the number of investments traded (bought and sold) within a day.
In this first version of the model, the fundamental value of the asset follows a random walk. To do so, a function is called to update the fundamental value using the following code:
fundamentalValue = fundamentalValue + normal(0.5, 0);
The market needs to store each bid and ask for the investment. In the model, I do this in a collection of bids and asks. Each bid and ask contains two data points: price, and the corresponding investor.
In the price history box, I keep track of how the investment characteristics change over time.
The market-agent
At the end of each day, the market solves all the investments’ order books. While the code to do so is a bit more complicated, the principle is simple. First, it looks at all entries of the investments’ order books. When there is a bid that has the same price or is higher than the price of the lowest ask, a transaction is made. After that, the market removes both entries from the order books and repeats the same cycle again.
This process is repeated until the condition is no longer met. After that, the market sets the price of the asset to the lowest ask price.
The investor-agent
The investor agent is where most of the intelligence will be added later. For now, each investor only has a collection of investments that he or she acquired. To trade on the market, each investor has the same basic function for placing orders.
for (Investment a : main.market.investments) {
double futurePriceEstimate = a.fundamentalValue + normal(1, 0);
if (portfolio.contains(a)) {
//place ask when owning the asset
a.asks.put(futurePriceEstimate, this);
} else
//place bid when not owning the asset
a.bids.put(futurePriceEstimate, this);
}
Each investor goes through all assets on the market and computes a random price based on the asset’s fundamental value. When the asset is already in the portfolio, the investor places an ask-order. If not, a bid-order is placed instead.
This resembles a super-rational investor with a standard estimation error. It knows exactly what the asset is worth and does not pay attention to any other market indicators.
Model behaviour
Let’s run a simple simulation with 10,000 investors and a single market investment over 100 days time. At time 0, the asset is added to 20% of the investor’s portfolios. Since the bid and ask prices are normally distributed, we expect the price to exceed the fundamental value. If 50% of the agents were given an asset instead, the price and fundamental value would largely coincide.
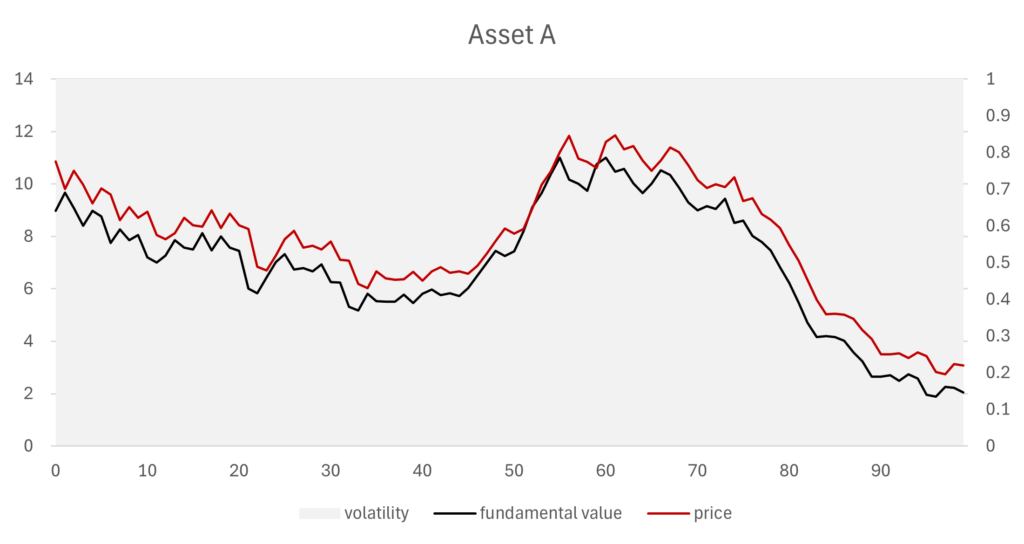
We see that our model seems to display the expected behaviour. Note that the volatility is equal to one, indicating that every possible ask-order is fulfilled. This is logical, given that the demand greatly exceeds the supply.
One Response